济南室内设计学校百度快照优化排名推广怎么做
目录
一、伪逆矩阵
◼ A的伪逆矩阵与SVD
◼ 用Python代码计算A的伪逆矩阵
◼ 笔算A的伪逆矩阵
一、伪逆矩阵
◼ A的伪逆矩阵与SVD
逆矩阵并不总是存在，即使是方阵。然而，对于非正方形矩阵，存在一个伪逆矩阵，也叫摩尔-彭罗斯逆矩阵。
例如，矩阵A是m×n。使用伪逆矩阵A^+，我们可以进行以下转换。
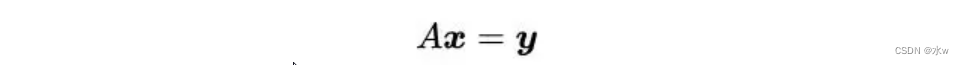
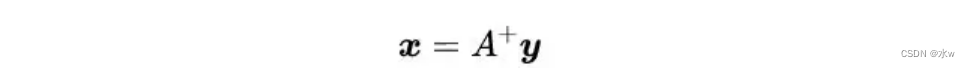
我们定义伪逆矩阵A^+为：
V和U来自奇异值分解。
我们通过转置Σ和所有对角元素的逆得到D^+。假设Σ的定义如下：
那么D+的定义如下：
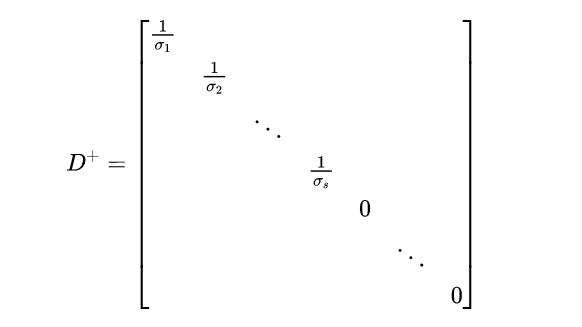
现在，我们可以看到A^+A的原理：
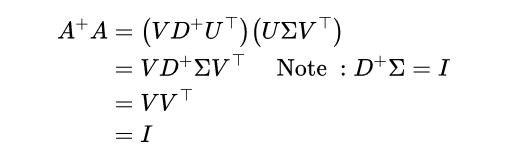
以同样的方式，AA^+ = I。
综上所述，如果我们能够对矩阵A进行奇异值分解，我们就可以通过VD^+UT来计算A^+，这是一个A的伪逆矩阵。
对于任意一个矩阵A，A的伪逆矩阵必然存在，且必然满足以下四个条件：
这四个条件(性质)蕴含了一个事情：AA^+必然是一个效果等同单位矩阵I、但又不是单位矩阵I的矩阵。
伪逆矩阵的极限形式定义：
伪逆矩阵更加常用的定义（基于SVD奇异值分解）
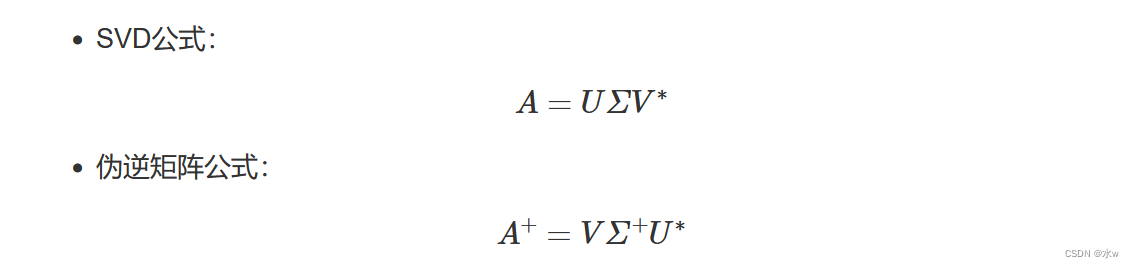
这个公式要注意的是中间的
的求法。因为
是一个对角线矩阵，但又不一定是方阵，所以计算它的伪逆矩阵的步骤是特殊又简单的：
-
将对角线上的元素取倒数
-
再将整个矩阵转置一次
◼ 用Python代码计算A的伪逆矩阵
让我们用Numpy试试伪逆矩阵吧，
import numpy as npA = np.array([[1, 2],[3, 4],[5, 6]], dtype=np.float64)
AP = np.linalg.pinv(A)
print('AP @ A')
print(AP @ A)下面是输出结果：
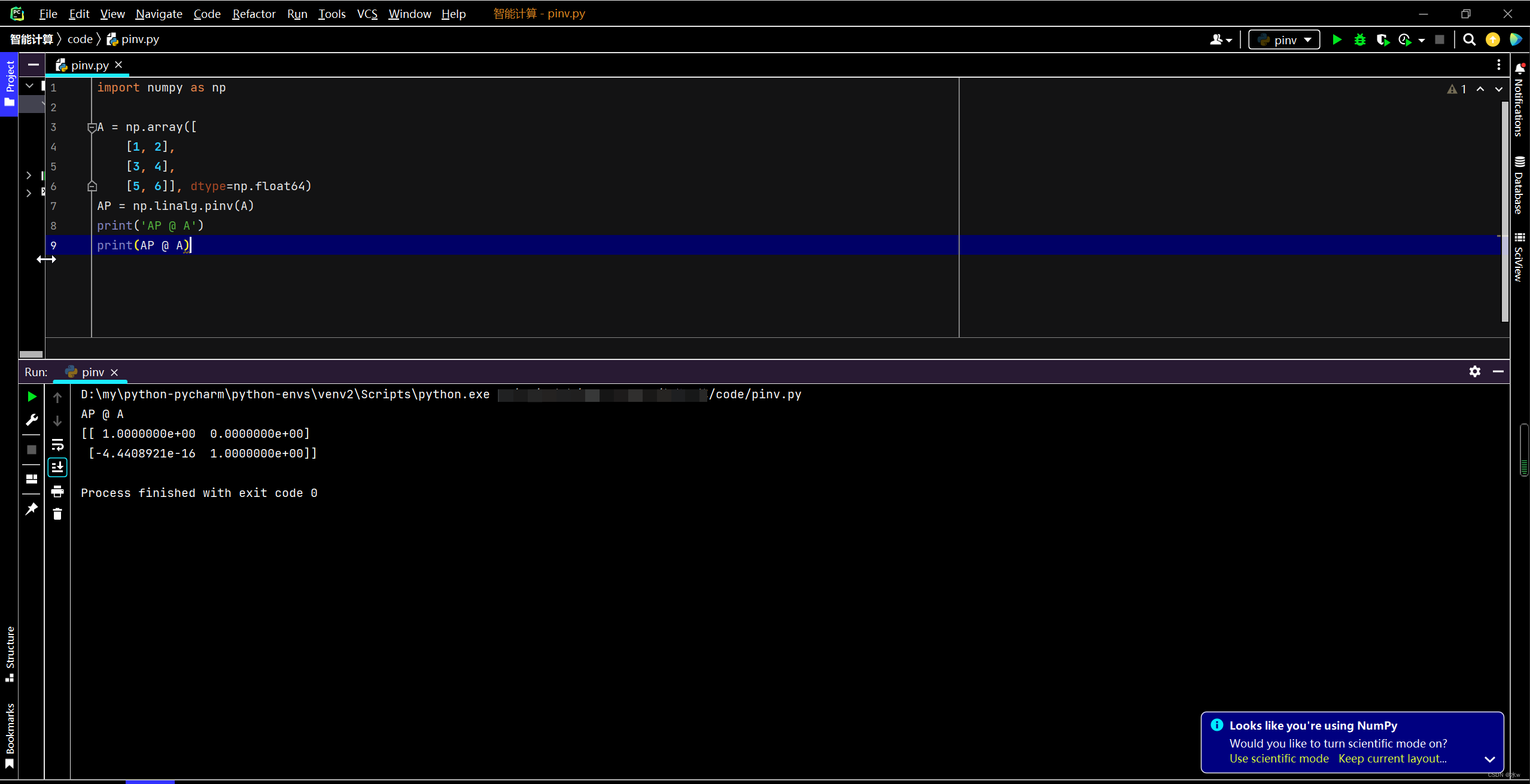
◼ 笔算A的伪逆矩阵
我们把矩阵 A 定义为：
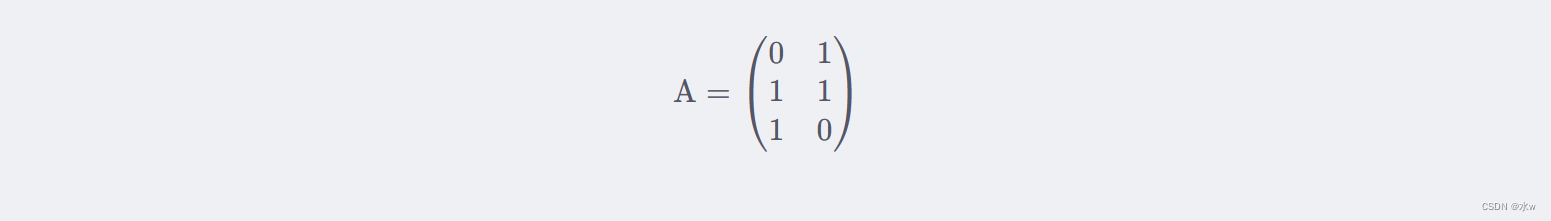
我们首先求出 A^TA 和 AA^T ,
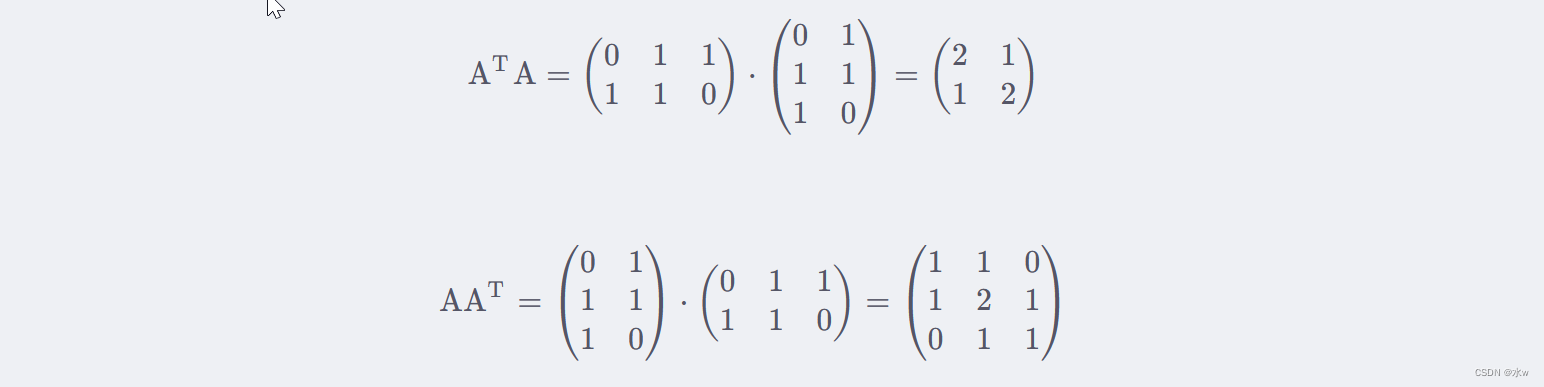
进而求出 A^TA 的特征值和特征向量：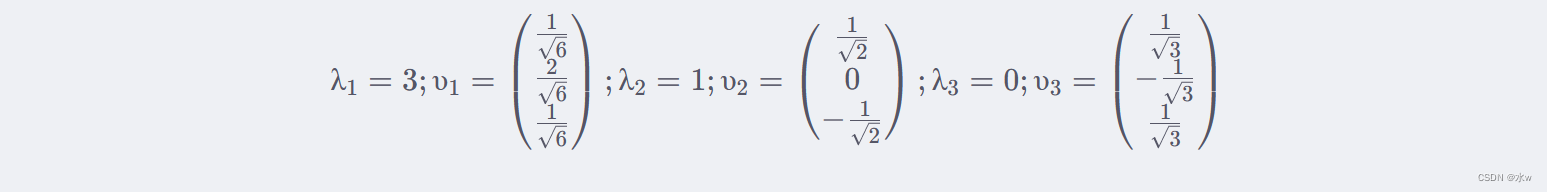
利用 Aνi=σiυi,i=1,2 求奇异值：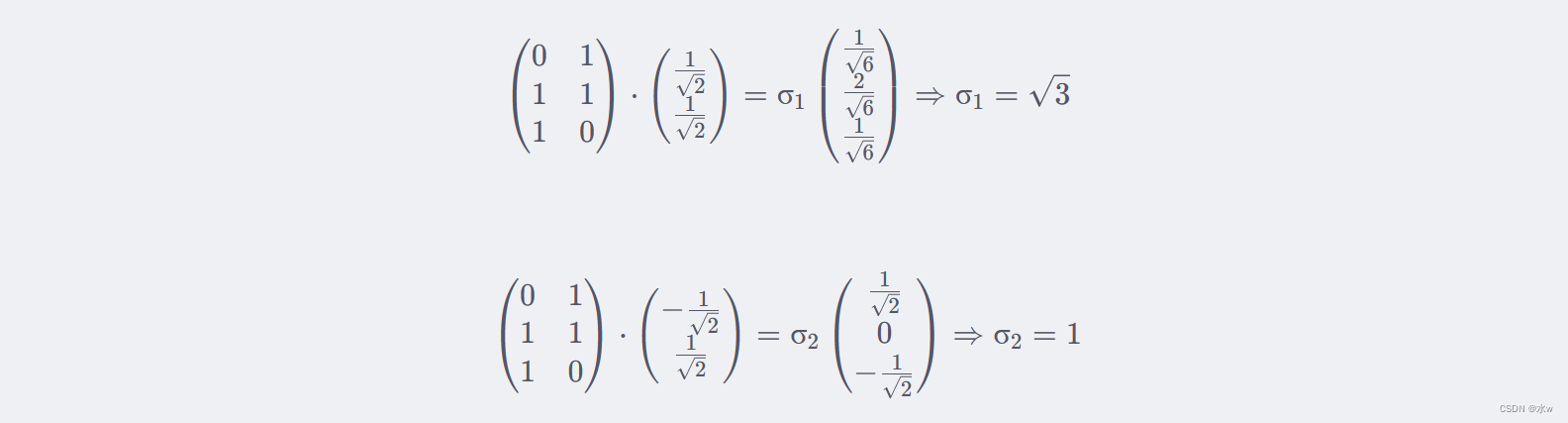
当然，我们也可以用 σ i =sqrt{ λ i }，直接求出奇异值为sqrt{3} 和 1。最终，可以得到 A 的奇异值分解为：
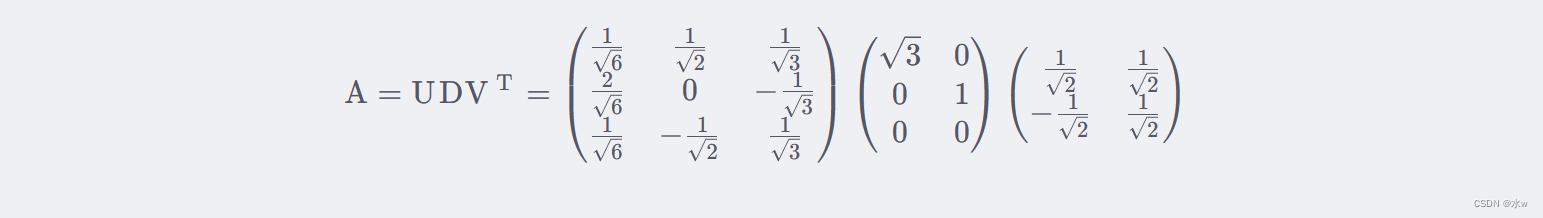
其中，矩阵 U ，D和 V 是矩阵 A奇异值分解后得到的矩阵。对角矩阵 D的伪逆 D^+ 是其非零元素取倒数之后再转置得到的。所以可以得到 A 的伪逆为：
